Crible de Mathiascevitch.cxx

adhoc

12/09/2023 à 18h17

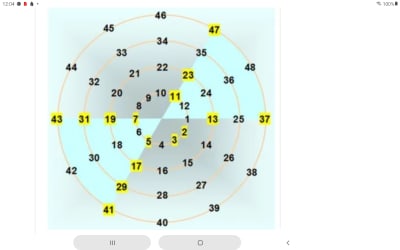
C'est absolument parfait, griffix, c'est de l'excellent travail, les index sont bien visibles, tu as mis une horloge. C'est de la tres belle oeuvre. Arriver a 100M des premiers nP comme en 1862, sans gros ordinateurs, tu m'as soufflé. Mattyiacevitch aussi :-) Le compte est bon.
J'ai a peu pres compris l'agorithme sur un plan informatique, mais sur le plan purement mathematique, comment ca fonctionne, je n'ai pas vraiment compris.
Je change de fusil d'epaule, je vais passer le programme recursif banal essentiellement utilisé en C, et voir combien de temps il faut. A mon avis beaucoup plus. Je ne suis pas a la retraite, ca va etre un peu plus long..... Et pour ne pas trop chercher d'excuse, difficile !!!!
Merci beaucoup beaucoup pour ton travail, ton temps et energie passés.

C’est moi qui ai apprécié tes encouragements.
J’ai eu une idée qui vaut certainement qqchose.
Les 6 boucles de recherche SONT TOTALEMENT INDÉPENDANTES.
D’où la possibilité de les faire tourner sur 6 bécanes ce qui réduirait le temps de travail pour rechercher les np d’une manière très importantes.
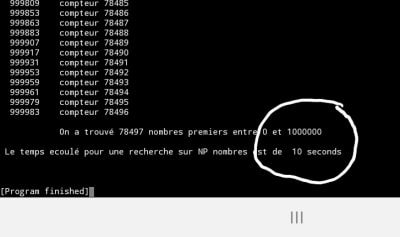
Le travail précédent sur un intervalle de 100millions durerait à peine 3mn40''.

adhoc

13/09/2023 à 09h44

Mon grand, j'ai une mission pour toi.
J'ai lu
"«Avec les ordinateurs, qui font des milliards d’opérations par seconde, la vitesse est faramineuse, mais, à partir d’un certain seuil, le disque sature. On arrive à calculer les nombres premiers jusqu’au 10^^24 ième environ. Après, ça bloque pour des questions de stockage», détaille Simon Plouffe."
Soit 24 chiffres apres le 1.
Je pense que ca ete fait avec l'algorithme un peu concon que j'utilise jusque la, de tester tous les diviseurs.
Il faudrait donc voir, avec ton algo amélioré, au bout de quoi le processeur ou la carrte mere ou le stockage plantent (ou la carte graphique si elle est type "gamers".
On rapelle que toutes les partules elementaires de l'univers connu tiendrait sur 100 chiffres.
Pour le moment, le milliard de chiffres a permis il ya peu de temps a une equipe d'obtenir un prix de 250000 dollars.
Le prix de 5M de dollars, c'est trouver par exemple le nombre premier d'index miliard de zeros apres 10 a partir d'une fonction sans faire appel a des matrices (tableaux).

Les nombres premiers ne peuvent être connus que dans une progression algorithmique et sont donc liés au temps.
De plus c’est complètement idiot de programmer des trucs inutiles car il est certain que les capacités de stockage seront limitées et on ne pourra jamais atteindre une limite qui de toute façon même si on avait les moyens techniques serait tjs incomplète.
Attendons donc que l’alpha et l’oméga se rejoignent et on saura tout sur le kiki le jour où le temps s’arrêtera !!!!
Comme disait Einstein on connaîtra la pensée de Dieu .............ou peut-être rien du tout après tout :)))))

Voici Adhoc le cœur de l’algorithme basé sur une simple observation.
Rien de vraiment mathématique !!!!!
Ça ressemblerait ti pas à de l’arithmétique modulaire ça par hasard!
Dans le fond pour sortir tous les premiers il n’y a pas besoin de faire des divisions ça sert à quedalle (dans mon programme il n’y a pas une seule division!!).
Seuls les tests sur un seul nombre en ont besoin.
Pour le reste :
On sort tous les multiples qu’on prend soin de ranger dans un tableau dont l’adresse correspond exactement à la valeur de ce nombre, car dans l’algorithme les multiples sortent d’une façon désordonnée. On voit ici l’intérêt d’avoir initialisé toutes les adresses de 0 à + l’infini avec le chiffre 0 car seules les adresses correspondantes aux nombres premiers n’auront pas été remplies par une valeur de nombre multiple.
Donc pour connaitre les nombres premiers il suffit de lire dans une boucle de 0 à l’infini toutes les cases du tableau et chaque fois que la valeur est égale à zéro on récupére l’adresse qui donne immédiatement le nombre premier correspondant.
La lecture dans ce second tableau de nombre premiers cette fois ci est totalement ordonné bien entendu et il n’est pas nécessaire d’utiliser une fonction de tri
Merci à 2 fois dans ton c... notamment et à son acolyte qui a bien su singer l’horloge du temps que j’ai mis ici en pièce jointe .
Salut mon ami adhoc, sur ce forum tu sors du lot une fois encore et la tête haute!
Merci mille fois.

Screenshot_20230823-120415_Samsung Internet.jpg

Screenshot_20230914-221542_Drive.jpg

Screenshot_20230909-183737.jpg

1a2ksnggdqf2cwy7nz18p50xtxtm.jpeg.jpg

Screenshot_20230915-140830_ColorNote.jpg

Fais toi plaisir adhoc
Les 2 premières fonctions A et B donnent TOUS LES NOMBRES PREMIERS avec TOUS leurs multiples
A = (6*i +1)
B = (6*i +5)
Les 4 fonctions suivantes C , D ,E , F donnent TOUS LEURS MULTIPLES sans les nombres premiers !!

C= (6*i + 11) * (6*i + 6*j + 11 )
D=(6*i + 7) * (6*i + 6*j + 7 )
E=(6*i + 11) * (6*i + 6*j + 13 )
F=(6*i + 7) * (6*i + 6*j + 11 )

Tu devines ce qui résulte de la séparation de ces ensembles (soustraction) ::
({A }+ {B}) - ({C} + {D} + {E} + {F}) ?????
Il restera malgré tout, les multiples de 5, mais ça je crois qu’on en crèvera pas!!!
On pourra rajouter 1 2 et 3 même si 1 n’est pas premier.
Ça me rappelle ce fil non?
https://forum.eugenol.com/sujets/430800-1-2-3-et-apres?page=1&scroll_to=post_1178357

Je me marre :)))))
Aujourd'hui j’aurais pas le temps.
Probablement que toi non plus mais au moins j’aurais sauvegardé.
Bye bye.
PS :
On retrouve ici le principe de la dualité et de la séparation de son contraire pour le retour à l’unité primordiale.
C’est exactement ce qui se passe en un instant dans les phénomènes mystiques!
Ce que fait l’ordinateur en réalisant des instructions en boucle inscrites dans le temps, l’esprit peut le faire en un instant immédiat inscrit dans l’éternité.
CQFD.

adhoc

19/09/2023 à 09h55

Resultat intéressant et tres original. Beau travail. Obtention des NP sans division mais par iterations et disjonctions ensemblistes. Vraiment, ce que j'ai hate de faire, c'est de prendre un programme "bateau" (tests des diviseurs) , et le comparer avec le tien. Ca se fera des que j'ai un peu de temps.

Ce soir mon travail tournera autour de ces 2 fonctions uniquement.
(6*i + 1)*(6*i + 1 + 6j)
(6*i + 1)*(6*i + 5 + 6j)
Pour i = 0 et j de 0 à l’infini on retrouve les 2 ensembles A et B précédents puis pour i >= 1 on devrait retrouver les 4 autres ensembles.
On simplifiera le programme au maximum.
Croisons les doigts.
Merci pour ton intérêt adhoc.

adhoc

19/09/2023 à 18h57

Je suis fan de tes travaux. Tant que tu peux optimiser, fais le (a ton rythme).

En fait je vais plutôt faire ceci.
(6*i + 1)*(6*j + 1)
(6*i + 1)*(6*j + 5)
(6*i + 5)*(6*j + 5)
Les chaînes de 6j +1 et 6j+1 avec i bloqué à 0 ci dessous

1 7 13 19 25 31 37 43 49.........
5 11 17 23 29 35 41 53 59........

Pour i = 0 on obtient tous les premiers avec leur multiple mis à part 2 et 3 ...donc pour 2 et 3 on s’en fout puisque les recherches pour un multiple de 3 se font avec un modulo ( concaténation de chaine) et 2 ma foi :))))))

En ouvrant le compteur pour i de 0 à l’infini et pour j également on obtient tous les multiples présents sur les chaînes 6×j + 1 et 6×j + 5..
L’un moins l’autre ben j’ose même pas imaginer :)))))
Je testerai ça dans la journée car j’ai un chiotte à installer.
Faut avoir la gueule dans la merde parfois .....ça redresse les idées.
Enfin je crois que cet Algo tu pourras t’en occuper. Tu es gardien des clés adhoc.
Ciao!!

adhoc

20/09/2023 à 08h38

>En fait je vais plutôt faire ceci.
(6*i + 1)*(6*j + 1)
(6*i + 1)*(6*j + 5)
Les chaînes de 6j +1 et 6j+1 avec i bloqué à 0 ci dessous

1 7 13 19 25 31 37 43 49.........
5 11 17 23 29 35 41 53 59........<

La , pour le moment , avec i bloqué a zéro, tu as simplement:
6j+1
6j+5

:-)

adhoc écrivait:
-----
> >En fait je vais plutôt faire ceci.
> (6*i + 1)*(6*j + 1)
> (6*i + 1)*(6*j + 5)
> Les chaînes de 6j +1 et 6j+1 avec i bloqué à 0 ci dessous
>
> 1 7 13 19 25 31 37 43 49.........
> 5 11 17 23 29 35 41 53 59........<
>
> La , pour le moment , avec i bloqué a zéro, tu as simplement:
> 6j+1
> 6j+5
>
> :-)
Avec j de1 à l’infini on a
donc les 2 chaînes du haut
exact....
Continue ....
Ps j’ai rajouté une chaîne voir plus haut

adhoc

20/09/2023 à 09h30

A tester, mais je pense que dans ton programme, tu peux eliminer les multiples de 5 avec le modulo %
if (maChaine%5 != 0)
{
....
}
c'est tres compact et tres rapide. Et tu peux l'crire dans une fonction. A voir.

Oui absolument !
Je vois tout ça ce soir. Merci
Pour pas perdre la methode précédente je vais d’abord l’appliquer de cette manière.

(6*i + 7)*(6*i + 6*j + 7) équivaut à (6*i + 1 )*(6*i + 6*j + 1)
(6*i + 7) * (6*i + 6*j + 11 ) équivaut a (6*i + 1 )*(6*i + 6*j + 5)
(6*i + 11)*(6*i + 6*j + 11 ) équivaut à (6*i + 5 )*(6*i + 6*j + 5)
(6*i + 11) * (6*i + 6*j + 13 ) équivaut à (6*i + 5) * (6*i + 6*j + 7 )
On va reprendre quasiment le même programme que précédemment sauf qu’on ne passera plus par les multiples de 3 et 5 et qu’on tiendra compte des 2 lignes de programme qui se résument en 6j +1 et 6j+5. Toutes les itérations suivantes ne sont que les calculs des multiples des nb premiers. C’est plus sûr d’utilser une méthode qui fonctionne déjà. 1 étant l’élément neutre pour la multiplication on retrouve ici quand i = 0 les fonctions (6j +1) * (1)et (6j + 5) * (1) .
D’ailleurs il est bien connu que tous les NP sont soit de la forme 6k + 1 ou 6k + 5.

adhoc

21/09/2023 à 10h49

>D’ailleurs il est bien connu que tous les NP sont soit de la forme 6k + 1 ou 6k + 5.<

Theoreme de Dirichlet !!!! :-))))

J'ai lu que les typers de programmes qui ressemblent au tien (cribles) sont 99.7 % plus rapides que les programmes bourrins qui testent tous les diviseurs de chaque nombre, jusqu'a 100 millions.
C'est sidérant. C'est super que tu te sois penché la dessus, j'apprends beaucoup, c'est génial !!!!!

adhoc écrivait:
-----
> >D’ailleurs il est bien connu que tous les NP sont soit de la forme 6k + 1 ou 6k
> + 5.<
>
> Theoreme de Dirichlet !!!! :-))))
>
> J'ai lu que les typers de programmes qui ressemblent au tien (cribles) sont
> 99.7 % plus rapides que les programmes bourrins qui testent tous les diviseurs
> de chaque nombre, jusqu'a 100 millions.
> C'est sidérant. C'est super que tu te sois penché la dessus, j'apprends
> beaucoup, c'est génial !!!!!

Je savais pas du tout Maurice :))))
Mais bon en évitant un maximum de test et de divisions je m’en doutais un peu. Pour l’instant je me dépêche de faire une salle de bain avant le mois de Novembre. Ça pourrait faire une division de la maison pour héberger un étudiant ou autre.
A plus adhoc, je vois ce soir pour la suite. En ce moment je bois une bière car je mouille ma chemise!!!! Ciao!!
Ps : ma fameuse horloge , idée qui m’est venue en début de nuit dans une cathédrale du Nord de la France et dont le programme s’inspire y est aussi pour qq chose.

6*i - 1)*(6*i - 1 + 6*j) ... 1 -5 -11
(6*i + 0)*(6*i + 0 + 6*j) ... 0 0 0
(6*i + 0)*(6*i + 1 + 6*j) ... 0 0 0
________________________________________________________________________________j_____
(6*i + 1)*(6*i + 1 + 6*j) ... -5 1 7 13 19 25 31 37 43 49
(6*i + 1)*(6*i + 5 + 6*j) ... -1 5 11 17 23 29 35 41 47
(6*i + 5)*(6*i + 5 + 6*j) ici les 4 fonctions incluent les nombres premiers
(6*i + 5)*(6*i + 7 + 6*j) par la multiplication par 1. Donc en poursuivant on finit par
obtenir la liste de tous les impairs premiers et non premiers (d’ailleurs les 2 premières fonctions en bloquant i à 0 suffisent déjà à trouver tous les impairs sauf les multiples de 2 et 3).
Je préfère utiliser 3 +2 +2 +2 .....c’est plus simple pour ce travail non?
On aura donc plus la possibilité d’extraire les nombres premiers
sauf en ayant recours aux 4 fonctions suivantes que j’ai utilisé dans
les programmes précédents ce qui ne présente pas grand intérêt.
En tout cas on retombe sur le théorème de Machin Chose qui montre bien que
les fonctions utilisées pour l’algorithme sont les bonnes!!!!! On gardera l’ancien programme c’est le mieux qu’on puisse faire pour l’instant.
_____________________________________________________________________________________
(6*i + 7)*(6*i + 7 + 6*j)
(6*i + 7)*(6*i +11+ 6*j)
(6*i +11)*(6*i +11+ 6*j)
(6*i + 11)*(6*i +13 + 6*j)

En ce qui concerne le prix à 5 millions de dollars pour faire un programme sans utiliser des tableaux équivaut à avoir trouvé une formule mathématique ni plus ni moins. Plutôt fumer autre chose que la moquette . On aura toutes les chances d’avoir plus vite un aperçu de ce que l’on recherche sans aucun effort!!!!!

Ça va beaucoup plus vite avec des Booléens
Tout est une histoire de False hard et de True duc :)))
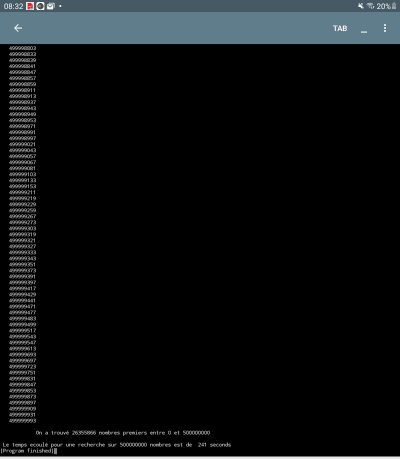
Pour 500 millions on a 241 secondes.

#include stdio.h
#include stdlib.h
#include math.h
#include conio.h
#include time.h
#include new


int main(int argc, char *argv[])
{

int a = 0;
int b =0;
int c =0;
int d =0;
int k =0;
int f =0;
int g =0;
int h =0;
int i =0;
int NP=0 ;
printf(" Saisir jusqu’à quelle valeur vous voulez rechercher les nombres Impairs Non Premiers et Premiers : \n\n\n ");
scanf(" %d",&NP);
time_t debut = time(NULL);

bool *Multiple = new bool [NP] ;
Multiple[0]= true;
Multiple[1]= true;

for (int x=0; x<= NP; x++)
{
Multiple[x] = false;
}


int sauvegarde =0;
int val1 =0;
int val2 = 0;
int val3 = 0;
int val4 = 0;
int val5 = 0;
int val6 =0;

suite:
b=0;
while (NP>= (6*a+ 7) * (6*a + 6*b + 7 ))
{

val1 = (6*a + 7) * (6*a + 6*b + 7 );

Multiple[val1] = true;
b++;
sauvegarde = b;

}
a++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite ;
}
else
{
printf("\n\n\n");
goto suite2;
}
suite2:

d = 0;
while (NP>= (6*c + 7) * (6*c + 6*d + 11 ))
{
val2 = (6*c + 7) * (6*c + 6*d + 11 );
Multiple[val2] = true;
d++;
sauvegarde = d;
}
c++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite2;
}
else
{
printf("\n\n\n");
goto suite3;
}
suite3:


k=2;
while (NP>= 3*k )
{
val3 = 3*k ;
Multiple[val3] = true;
k++;
}
printf("\n\n\n");

k=2;
while (NP>= 5*k )
{
val6 = 5*k ;
Multiple[val6] = true ;
k++;
}

printf("\n\n\n");


suite4:

g = 0;
while (NP>= (6*f + 11) * (6*f + 6*g + 11 ))
{
val4 = (6*f + 11) * (6*f + 6*g + 11 );
Multiple[val4] = true;
g++;
sauvegarde = g;
}
f++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite4;
}
else
{
printf("\n\n\n");
goto suite5;
}

suite5:

i = 0;
while (NP>= (6*h + 11) * (6*h + 6*i + 13 ))
{
val5 = (6*h + 11) * (6*h + 6*i + 13 );
Multiple[val5] = true;
i++;
sauvegarde = i;
}
h++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite5;
}

printf("\n\n\n LISTE DES NOMBRES PREMIERS : \n");

int sauv = 0;
int compteur = 1;

for (int z =3; z <= NP;z=z+2 )
{
if (!Multiple[z])
{
printf("\n %d " ,z);
compteur ++;
sauv = compteur -1;
}
}
printf ("\n\n On a trouvé %d nombres premiers entre 0 et %d", sauv, NP);
time_t fin = time(NULL);
printf("\n\n Le temps ecoulé pour une recherche sur %d nombres est de %d seconds", NP,(fin - debut));
}
}

Screenshot_20230925-083236.jpg

adhoc

25/09/2023 à 10h18

On ne voit pas tes include (balises >)
. C'est tres rapide, bravo!!!!

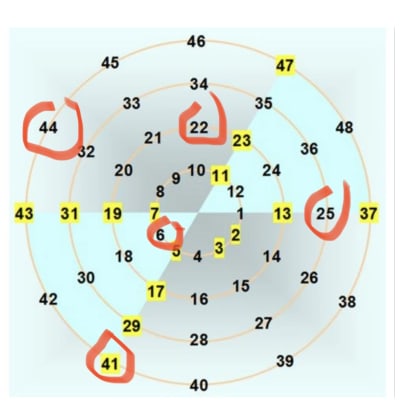
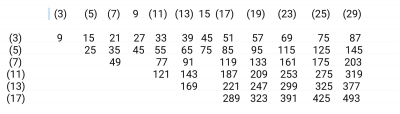
Une photo qui est plus explicite d’autres fonctions recursives possibles et plus simples :A ,B ,C ,D.
La première ligne donne tous les premiers avec leurs multiples.
Les lignes suivantes donnent tous les multiples possibles.
A+

Screenshot_20231009-222305_ColorNote.jpg

.

Ensemble de tous les multiples impairs X <= N

X = [[[[(3)+ 2] + 2] + 2] + 2] ......× (3) tant que X <= N
X = [[[[(5) +2] + 2] + 2] + 2] .......× (5) tant que X <= N
X = [[[[(7)+ 4] + 2] + 4] + 2] .......× (7) tant que X <= N
X = [[[(7 + 4) + 2] + 4] + 2] .......× (7 + 4) tant que X <= N
X = [[(7 + 4 + 2) + 4] + 2] .......× (7 + 4 + 2) tant que X <= N
X = [(7 + 4 + 2 + 4) + 2] .......× (7 + 4 + 2 + 4) tant que X <= N
etc etc

Screenshot_20231126-214001_ColorNote.jpg

Grifix-Gezucri écrivait:
--------------
> Ensemble de tous les multiples impairs X <= N
>
> X = [[[[(3)+ 2] + 2] + 2] + 2] ......× (3)
> tant que X <= N
> X = [[[[(5) +2] + 2] + 2] + 2] .......× (5)
> tant que X <= N
> X = [[[[(7)+ 4] + 2] + 4] + 2] .......× (7)
> tant que X <= N
> X = [[[(7 + 4) + 2] + 4] + 2] .......× (7 + 4) tant
> que X <= N
> X = [[(7 + 4 + 2) + 4] + 2] .......× (7 + 4 + 2) tant
> que X <= N
> X = [(7 + 4 + 2 + 4) + 2] .......× (7 + 4 + 2 + 4) tant que
> X <= N
> etc etc

Tu as donc survécu au 11 novembre. Content pour toi!

Merci bouboule.
11 Novembre pile poil ---> gros syndrome grippal avec hemoptysie !!!
Test Covid positif (c’est la première fois depuis la pandémie).
Tjs faiblard.
Merci encore.

Le Covid, c’est le premier qui fait mal, après on s’habitue ;-)