Une formule qui pue le soufre👹👹👹👹👹

#include stdio.h
#include stdlib.h

int main()
{
int val;
printf ( "\n Insérez la valeur sup de vos nombres : " ) ;
scanf("%d", &val);
bool * Tab = new bool [val];
int X=3,compteur=1;
while ( compteur>0)
{
for (int n =0 ; X*(X+2*n)< val ; n++)
{
Tab[X*(X+2*n)]=1;
compteur = n ;
}
X=X+2; compteur --;
}

int aff=0;
for (int i =3; i < val; i = i+2)
{
if (Tab[i]==0 )
{
printf("\t %d", i);
if ((aff++)%10==0)
printf("\n");
}
}
}

Screenshot_20240719-100903.jpg

adhoc

28/03/2024 à 09h19

C'est pas de l'Or , mais de la dynamite. Fais gaffe quand meme. Tu as poursuivui avec la formule des impairs non premiers. Fortiche.

adhoc écrivait:
-----
> C'est pas de l'Or , mais de la dynamite. Fais gaffe quand meme. Tu as poursuivui
> avec la formule des impairs non premiers. Fortiche.

C’est toujours un plaisir de t’avoir au bout du fil adhoc🤣🤣🤣🤣🤣

Screenshot_20240329-041742_ColorNote.jpg

C’est sympa d’avoir une formule qui donne tous les impairs non premiers à défaut de celle qui donne tous les impairs premiers non?
Maintenant que j’ai le Yin il ne me reste plus qu’à chercher le Yang🤣🤣🤣🤣

6550129.jpg

X(X + 2n)
On a ici une table de multiplication universelle des nombres impairs basée sur les carrés des nombres impairs par ordre croissant.

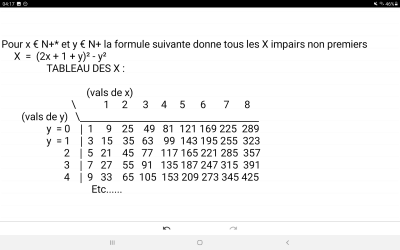
Pour x nb entier defini sur [1, +∞[ et y nb entier défini sur [0, +∞[ la formule suivante donne TOUS les X impairs non premiers
X = (2x + 1 + y)² - y²
Chaque multiple peut donc être défini par un couple (x,y)
On trouve tjs dans ce cas un couple avec x=0 et y≠0 et au moins un x≠0 et y défini sur l’intervalle [0, +∞[
Dans le cas d’un nb premier on a UN seul couple du type (0, y≠0) .
(1,0) (2,0) (3,0) (4,0)...... <=> 9 25 49 81 121.....
(1,1) (2,1) (3,1) (4,1)...... <=> 15 35 63 99 143....
(1,2) (2,2) (3,2) (4,2)...... <=> 21 45 77 117 165 .....
(1,3) (2,3) (3,3) (4,3)...... <=> 27 55 91 135.....
(1,4) (2,4) (3,4) (4,4)...... <=> 33 65 105 153.....

Dans le cas des multiples impairs on a au moins 2 couples:

(1,0)=(0,4) = 9 ; (2,0)=(0,12)=25 ; (3,0)=(0,24) =49 ; (4,0)=(0,40) = 81 ; (5,0)=(0,60)= 121
(1,1)=(0,7) = 15 ; (2,1)=(0,17) =35 ; (3,1)=(0,31) =63 ; (4,1)=(0,49)=99 ; (5,1)=(0,71)=143
(1,2)=(0,10) = 21 ; (2,2)=(0,22)=45
(1,3)=(0,13) = 27 ; (2,3)=(0,27)=55
(1,4)=(0,16) = 33 ; (2,4)=(0,32)=65
(1,5)=(0,19)= 39 ;

Pour trouver les valeurs des couples X= (0, ?) , en remplaçant par x=0 on obtient :
X= (2×0 +1 +y)² - y²
X= (y+1)² - y²
X= 2y + 1
y = (X-1) / 2

Rigolo!!!!

J’ai perdu un peu mon temps......enfin presque🤣🤣🤣!!!
J’ai optimisé la recherche sur 800 millions en la réalisant en 3 fois moins de temps soit 24 secondes au lieu de 76 secondes.
Puis j’ai optimisé la mémoire en la stockant non plus sur un octet mais sur 1 bit mémoire, et j’ai pu calculer ainsi les NP sur un espace de 2 Milliards en 96 secondes.

Screenshot_20241016-144521_Chrome.jpg

Screenshot_20241016-143157.jpg

Screenshot_20241016-144325.jpg

Screenshot_20241016-142225.jpg

#include stdio.h
#include stdlib.h
#include time.h
#include new

int main()
{
long int compteur = 1, x = 1, a =3 , val, comptage = 1;
int choix;
printf("Programme Grifix de recherche des NP non optimisé"
" \nRechercher tous les nbres premiers en dessous de val = ");
scanf("%ld", &val);
time_t debut = time(NULL);
bool *Tableau = new bool[val];
while (compteur > 0)
{
int n = 0 ;
long int b =a*a ;
while ( b + n*2*a < val)
{
Tableau[ b + n*2*a ] = 1;
compteur = n++;
}
x++;
a = 2*x +1;
compteur--;
}

time_t fin = time(NULL);
printf("\nRecherche terminée en %d secondes ", fin - debut);
for (int i = 3; i < val; i = i + 2)
{
if (Tableau[i] == 0)
{
comptage++;
}
}
printf(" \n Il y a % ld NP entre 1 et %ld", comptage, val);
printf("\n\nChoix 1 = Sortir ou Choix 2 = Afficher liste : ");
scanf("%d", &choix);
if (choix == 1)
{
exit(EXIT_SUCCESS);
}
else
printf("2");
for (int i = 3; i < val; i = i + 2)
{
if (Tableau[i] == 0)
{
printf(" %d", i);
}
}
}

#include stdio.h
#include stdlib.h
#include time.h

int main()
{
int val;
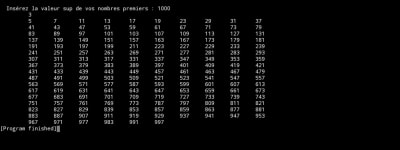
printf ( "\n (Programme Grifix programme de recherche des Nombres Premiers optimisé) \n Insérez la valeur sup de vos nombres : " ) ;
scanf("%d", &val);
bool * Tab = new bool [val];
int X= 3 ;
int compteur=1,boucle = 1;
int nombre_de_premiers=0;
time_t debut = time(NULL);
printf(" boucle : %d ", 1);
while ( compteur>0)
{
for (int n =0 ; X*(X+2*n)< val ; n++)
{
if (Tab[X]==0)
{
Tab[X*(X+2*n)]=1;
compteur = n ;
printf(" \n X=%d compteur = %d multiple %d ",X, compteur, X*(X +2*n));
}
else
{
printf ( "\n Saut de boucle else pour X=%d", X) ;
goto suite;
}
}
 

suite: X=X+2;
compteur --;
boucle++;
printf(" \n boucle : %d", boucle) ;
}
time_t fin = time(NULL);
printf ("\nTemps de recherche : %d secondes \n ", fin- debut);
for (int i =3; i < val; i = i+2)
{ if (Tab[i]==0 )
{
nombre_de_premiers ++;
// printf (" %d", i);
}
}
printf(" On a trouvé %d nombres premiers", nombre_de_premiers);
}

POUR TESTER LA RAPIDITÉ DU PROG ON SUPPRIME LES FONCTIONS D’AFFICHAGE

#include stdio.h
#include stdlib.h
#include time.h

int main()
{
int val;
printf ( "\n (Programme Grifix programme de recherche des Nombres Premiers optimisé sans affichage ) \n Insérez la valeur sup de vos nombres : " ) ;
scanf("%d", &val);
bool * Tab = new bool [val];
int X= 3 ;
int compteur=1;
int nombre_de_premiers=0;
time_t debut = time(NULL);
while ( compteur>0)
{
for (int n =0 ; X*(X+2*n)< val ; n++)
{
if (Tab[X]==0)
{
Tab[X*(X+2*n)]=1;
compteur = n ;
}
else
{
goto suite;
}
}
 

suite: X=X+2;
compteur --;

}
time_t fin = time(NULL);
printf ("\nTemps de recherche : %d secondes \n ", fin- debut);
for (int i =3; i < val; i = i+2)
{ if (Tab[i]==0 )
{
nombre_de_premiers ++;
}
}
printf(" On a trouvé %d nombres premiers", nombre_de_premiers);
}

Programme incluant une gestion memoire sur des bits pour atteindre 2 Milliards.

#include stdio.h
#include stdlib.h
#include time.h

int main()
{
int val;
printf ( "\n (Programme Grifix programme de recherche des nombres premiers optimisé avec amelioration gestion memoire sur des bits) \n Insérez la valeur sup de vos nombres : " ) ;
scanf("%d", &val);
unsigned char *Tab = (unsigned char *)malloc((val + 7) / 8); // On alloue le nombre de bits nécessaires
if (Tab == NULL)
{
printf("Erreur d'allocation de mémoire\n");
}
int X= 3 ;
int compteur=1;
int nombre_de_premiers=0;
time_t debut = time(NULL);
while ( compteur>0)
{
for (int n =0 ; X*(X+2*n)< val ; n++)
{
if (!(Tab[X / 8] & (1 << (X % 8))))
{
Tab[X*(X +2*n) / 8] |=(1 << (X*(X +2*n) % 8));
compteur = n ;
}
else
{
// printf("\n saut pour X= %d", X);
goto suite;
}
}
 

suite: X=X+2; compteur --;
}
time_t fin = time(NULL);
printf ("\nTemps de recherche : %d secondes \n ", fin- debut);
for (int i =3; i < val; i = i+2)
{ if ((Tab[i / 8] & (1 << (i % 8))) ==0)
{
nombre_de_premiers ++;
// printf (" %d", i);
}
}
printf(" On a trouvé %d nombres premiers", nombre_de_premiers);
free(Tab); // Libération de la mémoire allouée
}

Ce code C est un programme optimisé pour trouver les nombres premiers jusqu'à une valeur donnée. Voici une explication du code :

Inclusions de fichiers d'en-tête :
#include : Permet l'utilisation de fonctions d'entrée/sortie standard comme printf et scanf.
#include : Fournit des fonctions pour l'allocation de mémoire dynamique comme malloc et free.
#include : Permet de mesurer le temps d'exécution du programme.
Fonction main :
Le point d'entrée du programme.
Entrée de l'utilisateur :
Demande à l'utilisateur de saisir la valeur supérieure de la plage de nombres à tester.
Stocke la valeur saisie dans la variable val.
Allocation de mémoire :
Alloue un bloc de mémoire dynamique pour un tableau de caractères non signés (unsigned char *Tab).
La taille du tableau est calculée comme le nombre de bits nécessaires pour représenter tous les nombres jusqu'à val.
Si l'allocation échoue, un message d'erreur est affiché et le programme se termine.
Initialisation des variables :
X : Initialise le premier nombre impair à tester (3).
compteur : Initialise un compteur pour la boucle principale.
nombre_de_premiers : Initialise un compteur pour le nombre de nombres premiers trouvés.
Mesure du temps de début :
Enregistre le temps actuel à l'aide de la fonction time(NULL) et le stocke dans la variable debut.
Boucle principale :
Itère jusqu'à ce que compteur devienne inférieur ou égal à 0.
Boucle interne :
Itère sur les multiples de X jusqu'à ce qu'ils dépassent val.
Vérification de la primalité :
Si le bit correspondant au nombre actuel dans le tableau Tab n'est pas défini (c'est-à-dire que le nombre n'est pas marqué comme non premier), il est marqué comme non premier en définissant le bit correspondant dans Tab.
compteur est mis à jour avec la valeur de n pour la prochaine itération.
Si le bit correspondant est déjà défini, cela signifie que le nombre est déjà marqué comme non premier, et la boucle interne est interrompue en utilisant goto suite.
Incrémentation de X :
X est incrémenté de 2 pour passer au prochain nombre impair.
compteur est décrémenté.
Mesure du temps de fin :
Enregistre le temps actuel à l'aide de la fonction time(NULL) et le stocke dans la variable fin.
Affichage du temps d'exécution :
Affiche la différence entre fin et debut en secondes.
Comptage des nombres premiers :
Parcourt tous les nombres impairs de 3 à val.
Si le bit correspondant dans Tab n'est pas défini, cela signifie que le nombre est premier, et nombre_de_premiers est incrémenté.
Affichage du nombre de nombres premiers trouvés :
Affiche le nombre total de nombres premiers trouvés.
Libération de mémoire :
Libère le bloc de mémoire alloué à Tab à l'aide de la fonction free(Tab).
Explication de l'optimisation de la gestion de la mémoire :

Le code utilise un tableau de bits (Tab) pour représenter tous les nombres jusqu'à val. Chaque bit dans le tableau correspond à un nombre, et un bit défini indique que le nombre correspondant est non premier.
Cette approche est plus efficace en termes de mémoire que de stocker tous les nombres dans un tableau.
La taille du tableau Tab est calculée comme le nombre de bits nécessaires pour représenter tous les nombres jusqu'à val, ce qui permet d'optimiser l'utilisation de la mémoire.
Explication du code optimisé :

Le code utilise le crible d'Ératosthène pour identifier les nombres premiers.
La boucle principale itère sur les nombres impairs à partir de 3.
Pour chaque nombre impair X, la boucle interne itère sur ses multiples jusqu'à ce qu'ils dépassent val.
Si un multiple de X n'est pas encore marqué comme non premier, il est marqué comme non premier en définissant le bit correspondant dans Tab.
La boucle interne est interrompue si un multiple de X est déjà marqué comme non premier, car tous les multiples suivants de X seront également non premiers.
Cela permet d'optimiser le processus en évitant de vérifier les multiples de nombres déjà marqués comme non premiers.
En résumé, ce code C est une implémentation efficace du crible d'Ératosthène pour trouver les nombres premiers jusqu'à une valeur donnée, en utilisant une gestion optimisée de la mémoire pour un meilleur rendement.

Code en Java script pour l’ami adhoc grâce à l’IA.

function findPrimes(val) {
// Alloue le nombre de bits nécessaires
const tab = new Uint8Array(Math.ceil((val + 7) / 8));
let x = 3;
let compteur = 1;
let nombreDePremiers = 0;
const debut = Date.now();

while (compteur > 0) {
for (let n = 0; x * (x + 2 * n) < val; n++) {
if (!(tab[x / 8] & (1 << (x % 8)))) {
tab[x * (x + 2 * n) / 8] |= (1 << (x * (x + 2 * n) % 8));
compteur = n;
} else {
// Saut pour X = x
continue;
}
}
x += 2;
compteur--;
}

const fin = Date.now();
console.log(`Temps de recherche : ${fin - debut} millisecondes`);

for (let i = 3; i < val; i += 2) {
if (!(tab[i / 8] & (1 << (i % 8)))) {
nombreDePremiers++;
// console.log(` ${i}`);
}
}

console.log(`On a trouvé ${nombreDePremiers} nombres premiers`);
}

const val = 1000;
findPrimes(val);
Explications :

Allocation de mémoire : En JavaScript, on utilise un Uint8Array pour représenter le tableau de bits.
Opérations sur les bits : Les opérations de décalage de bits (<< et >>) et de masque de bits (& et |) sont les mêmes en JavaScript qu'en C.
Gestion du temps : On utilise Date.now() pour mesurer le temps de recherche en millisecondes.
Affichage des résultats : On utilise console.log() pour afficher les résultats dans la console.
Points importants :

Le code JavaScript utilise les mêmes algorithmes que le code C.
La gestion de la mémoire est automatique en JavaScript, il n'est donc pas nécessaire d'utiliser free().
Le code JavaScript est plus concis que le code C.
Remarques :

Le code C utilise goto pour sauter à une étiquette, ce qui n'est pas recommandé en JavaScript.
Le code JavaScript utilise des commentaires pour expliquer les différences avec le code C.

adhoc

16/10/2024 à 13h57

Tu as fait un tableau de bits pour marquer les nombres premiers et non-premiers. Tres fort.
Tu as essayé le code en JS ou tu veux que je mette sur mon serveur pour essai?

adhoc

16/10/2024 à 14h13

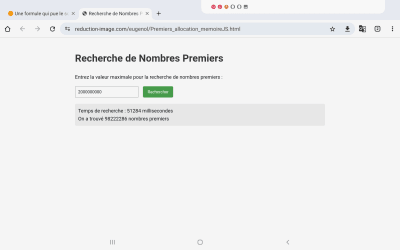
J'ai mis ton programme JS, en production
https://reduction-image.com/eugenol/Premiers_allocation_memoireJS.html
Impressionnant, le crible d'erasthotene modifié. Et impressionnant aussi que ca soit un dentiste qui arrive a ces resultats. Bravo.

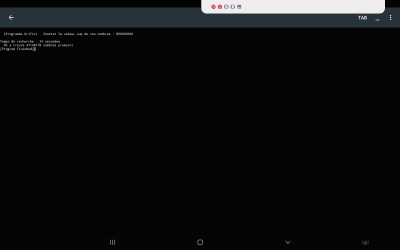
Non, ce qui est impressionnant c’est qu’en JS tu mettes 2 fois moins de temps jusqu'à 2Milliards !!!!!
Voir saisie d’écran
Je suis epatatassé.
Bye mon grand pote,👋👋

Screenshot_20241016-163200_Chrome.jpg

adhoc

16/10/2024 à 15h03

C'est TON programme que l'IA a adapté. Seul, sans rien lui dire de specifique, il aurait pondu une merdouille.
2500000000
Rechercher
Temps de recherche : 75893 millisecondes
On a trouvé 121443370 nombres premiers
1minute et demie pour les deux et demi premiers milliards de nombres. pitine..... Je suis scotché. Mon ordi ,dans mon cab est tres moyen, il a 8 ans..... Je ne te dis pas avec un ordi meuh meuh de maintenant.

adhoc écrivait:
-----
> C'est TON programme que l'IA a adapté. Seul, sans rien lui dire de specifique,
> il aurait pondu une merdouille.
> 2500000000
> Rechercher
> Temps de recherche : 75893 millisecondes
> On a trouvé 121443370 nombres premiers
> 1minute et demie pour les deux et demi premiers milliards de nombres.
> pitine..... Je suis scotché. Mon ordi ,dans mon cab est tres moyen, il a 8
> ans..... Je ne te dis pas avec un ordi meuh meuh de maintenant.

Il n’y a rien eu de spécial seulement une petite idée née de l’observation il y a 3 jours vers 4 h du mat.
Ah si !! Le traitement de la mémoire ralenti de bien 30% le travail...dommage.
Bonne fin de journée!

Quand une idée en amène une autre.....
L’observation que j’ai faite pour optimiser vient du fait que toutes les boucles multiplicatives partent des carrés sur les impairs successifs soient 3² 5² 7² 9² 11² 13² 15² etc etc
Il est évident qu’il ne sert à rien de partir sur des boucles de multiples déjà identifiés comme 9 15 21 25 27 etc etc car la décomposition en facteur premier de ces multiples ramène toujours à un multiple déjà identifié en amont.
Ici 2 Exemples:
9² = 3×3×3×3 ou bien 3×27 = 81 qui a été identifié dans la première boucle de 3²
15²= 3×5×3×5 = 225 qui a été identifié 2 fois dans la boucle sur 3² => 3×75=225 et dans la boucle sur z5² => 5×45= 225.
Donc supprimer les carrés sur des multiples déjà identifiés m’a permis d’aller 3 fois plus vite!!
Mais si on est attentif à ces 2 exemples on voit de suite que l’on aimerait supprimer d’autres doublons !!!!
Ici il est évident que 225 se retrouve 2 fois ..... une fois dans la boucle sur 3² et une autre dans la boucle sur 5².
J’ai programmé cette suppression pour éviter TOUS les doublons calculés mais ces tests avant de pouvoir eviter la multiplication inutile sont consommateurs en ressource et font perdre plus de temps que la multiplication proprement dite!!!
Les premiers résultats sont décevants.
On arrive à un paradoxe qui est le suivant: on doit absolument calculer les multiples d’un multiple pour qu’il ne soit pas identifié comme un nombre premier et en même temps on cherche à éviter son calcul pour gagner du temps!!!!
Pour résumer la situation on aimerait que la définition d’un booléen en C évolue un peu pour aboutir à une optimisation maximum.
On sait déjà qu’incrémenter un booléen avec n’importe quelle valeur entière positive comme dans ces écritures ci dessous donne toujours une valeur vraie
Bool Vraifaux = 567 ou Vraifaux = 3 ou Vraifaux = 1 donne toujours une valeur booléenne à vrai ou équivalente à Vraifaux == 1
Bool Vraifaux = 0 donnera toujours une valeur booléenne à faux ou équivalente à Vraifaux == 0 .
L’ avantage de la variable booléenne c’est qu’elle consomme peu de mémoire et pourtant on aimerait pour sortir de l’impasse qu’elle donne une valeur vrai tout en gardant les valeurs entieres telles que 567 ou 3 rentrées précédemment pour éviter des tests consommateurs de ressources.
On est dans l’APORIE TOTALE🤣🤣🤣🤣
Vitesse ou consommation mémoire, voilà le deal!

Essayes ce code JS adhoc je pense qu’il sera meilleur!
function main() {
const val = parseInt(prompt("Entrez la valeur supérieure de vos nombres : "));

// Allocation de mémoire pour le tableau de bits
const bitArray = new Array((val + 7) / 8).fill(0);

// Marquer les multiples de 2 et 3
for (let i = 4; i <= val; i += 2) {
bitArray[i / 8] |= 1 << (i % 8);
}
for (let i = 6; i <= val; i += 3) {
bitArray[i / 8] |= 1 << (i % 8);
}

// Marquer les multiples des nombres premiers restants
for (let i = 5; i * i <= val; i += 6) {
if (!(bitArray[i / 8] & (1 << (i % 8)))) {
for (let j = i * i; j <= val; j += i) {
bitArray[j / 8] |= 1 << (j % 8);
}
for (let j = i + 2; j * j <= val; j += i) {
if (!(bitArray[j / 8] & (1 << (j % 8)))) {
for (let k = j * j; k <= val; k += j) {
bitArray[k / 8] |= 1 << (k % 8);
}
}
}
}
}

// Compter les nombres premiers
let nombreDePremiers = 1; // On compte '2' comme premier
for (let i = 3; i < val; i += 2) {
if (!(bitArray[i / 8] & (1 << (i % 8)))) {
nombreDePremiers++;
}
}

// Calculer le temps de recherche
const startTime = new Date().getTime();
const endTime = new Date().getTime();
const searchTime = (endTime - startTime) / 1000;

console.log(`\nTemps de recherche : ${searchTime} secondes`);
console.log(`On a trouvé ${nombreDePremiers} nombres premiers`);
}

main();

adhoc

18/10/2024 à 08h15

Des que je peux, on passe ton programme en production !!!

adhoc

18/10/2024 à 09h11

J'ai peur que ca soit un peu plus lent (pas de beaucoup)
https://reduction-image.com/eugenol/Premiers_allocation_memoireJS2.html

Le precedent etait le meme url, sauf le 2

https://reduction-image.com/eugenol/Premiers_allocation_memoireJS.html

Element rassurant: on retrouve le meme nombre de NP pour les deux versions.

Exact Pourtant je gagne 10 s en C sur 2 Milliards
Cette AI c’est une grosse feignasse !!!
Bonne journée je te dérange plus, merci bcp!
Sinon en C bcp plus simple:

#include stdio.h
#include stdlib.h
#include time.h

int main() {
int val;
printf("\n(Programme Grifix - recherche des nombres premiers optimisé)\nInsérez la valeur sup de vos nombres : ");
scanf("%d", &val);

// Allocation de mémoire pour le tableau de bits
unsigned char *Tab = (unsigned char *)calloc((val + 7) / 8, sizeof(unsigned char));
if (Tab == NULL) {
printf("Erreur d'allocation de mémoire\n");
return 1;
}

int X = 3;
int nombre_de_premiers = 1; // On compte '2' comme premier
time_t debut = time(NULL);

// Parcours des nombres impairs pour marquer les non-premiers
for (X = 3; X * X <= val; X += 2) {
// Si X est un nombre premier (non marqué)
if (!(Tab[X / 8] & (1 << (X % 8)))) // ICI LA CLÉ DE L’OPTIMISATION
{
// Marquer les multiples impairs de X à partir de X*X
for (int n = X * X; n < val; n += 2 * X)
{
Tab[n / 8] |= (1 << (n % 8));
}
}
}

// Calcul du nombre de premiers
for (int i = 3; i < val; i += 2) {
if ((Tab[i / 8] & (1 << (i % 8))) == 0) {
nombre_de_premiers++;
}
}

time_t fin = time(NULL);
printf("\nTemps de recherche : %ld secondes\n", fin - debut);
printf("On a trouvé %d nombres premiers\n", nombre_de_premiers);

free(Tab); // Libération de la mémoire allouée
return 0;
}

adhoc

18/10/2024 à 13h42

Ce qui est etonnant , c'est que le deuxieme propgramme en JS va plus vite pour 2 MM alors qu'il est plus lent (relativement) pour un traitement plus petit en nombres On passe de 48 pour JS1 a 46 pour JS2.Comme pour tes 2 progs en C C'est lié a la facon dont les NP sont stockés Ce qu'on perd au depart , on le regagne par la suite.