Une formule qui pue le soufre👹👹👹👹👹

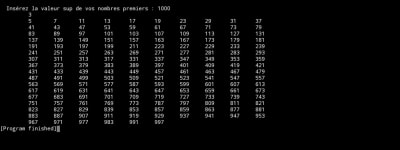
#include stdio.h
#include stdlib.h
#include new

int main()
{
int val;
printf ( "\n Insérez la valeur sup de vos nombres premiers : " ) ;
scanf("%d", &val);
bool * Tab = new bool [val];
// RECHERCHE DE TOUS LES MULTIPLES
int a=3,c=1;
while ( c>0)
{
for (int b =0 ; a*(a+b)< val ; b=b+2)
{
Tab[a*(a+b)]=1;
c= b/2;
}
a=a+2; c--;
}

// AFFICHAGE DES NOMBRES PREMERS-
int aff=0;
for (int i =3; i < val; i = i+2)
{
if (Tab[i]==0 )
{
printf("\t %d", i);
if ((aff++)%10==0)
printf("\n");
}
}
}

Screenshot_20240719-100903.jpg

adhoc

28/03/2024 à 10h19

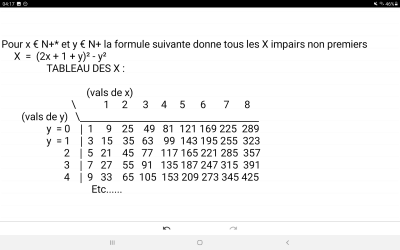
C'est pas de l'Or , mais de la dynamite. Fais gaffe quand meme. Tu as poursuivui avec la formule des impairs non premiers. Fortiche.

adhoc écrivait:
-----
> C'est pas de l'Or , mais de la dynamite. Fais gaffe quand meme. Tu as poursuivui
> avec la formule des impairs non premiers. Fortiche.

C’est toujours un plaisir de t’avoir au bout du fil adhoc🤣🤣🤣🤣🤣

Screenshot_20240329-041742_ColorNote.jpg

C’est sympa d’avoir une formule qui donne tous les impairs non premiers à défaut de celle qui donne tous les impairs premiers non?
Maintenant que j’ai le Yin il ne me reste plus qu’à chercher le Yang🤣🤣🤣🤣

6550129.jpg

a(a+b)
On a ici une table de multiplication universelle des nombres impairs basée sur les carrés des nombres impairs par ordre croissant.