Tous les forums
Problèmes et énigmes à résoudre...Bonne chance
20/06/2015 à 12h10
bon là je fais partir la corde depuis un sommet du triangle et je suis en train de me dire que si la corde ne part pas d'un sommet ça complique tout......
mon adhoc, tu nous programmes ça: tracer d'une corde disposée aléatoirement, calcul de sa longueur est comparaison avec celle du côté du triangle, cela sur un grand nombre de cordes et on aura une approche du résultat :)
20/06/2015 à 12h22
Arf mon growly, ton approche géométrique est sympa. J'aime beaucoup!
Si trymartin ne repond pas (il doit pioncer, je crois que notre ami est dans les iles), on va aller chercher la formule de la longueur du coté d'un triangle equilatéral inscrit dans un cercle par rapport au rayon, et puis voila! :-)
20/06/2015 à 12h56
bon alors moi j'essaie de déterminer la façon de calculer une corde aléatoire.
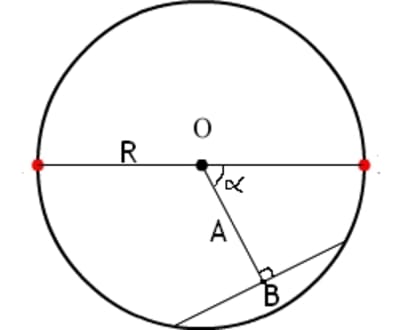
j'émets l'hypothèse qu'une corde peut avoir comme caractéristique unique la longueur A du segment qui passe par le milieu du cercle et qui coupe perpendiculairement cette corde et par l'angle alpha qui existe entre ce segment et un diamètre fixe référence.
la longueur c de la corde doit pouvoir se calculer en fonction de alpha et de la longueur A de ce segment. Donc si on choisi aléatoirement alpha et A on va déterminer des longueur de cordes aléatoires. (je m'efforce de ne pas googueliser sinon ça n'aurait plus de charme :)
20/06/2015 à 13h32
Tu as le cercle trigonométrique deja fait , mon growly.
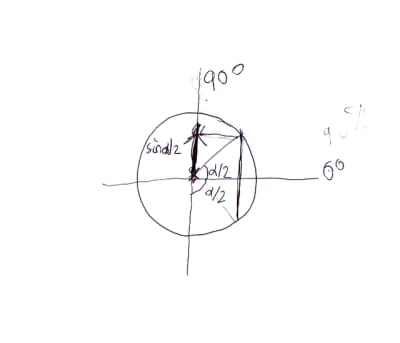
Trace une corde moyenne verticale a droite, . Tu verras que la projection de la moitié de ta corde sur l'axe vertical est le sinus de ton angle trigonométrique alpha.
La tout est de faire varier l'angle trigonométrique de 0 radian (le point) vers Pi/2 rad (90 degrés la rayon) pour voir la longueur moyenne de cette moitié de corde!
On prend 45 degrés comme valeur moyenne , et on a la moyenne de la demi corde.
Je suis au cab, mon dessin est moche, je n'ai qu'un style noir avec moi, mais on s'en fiche!
20/06/2015 à 13h52
growler écrivait:
-----------------
> et je ne saurais le démontrer autrement que par un dessin
sauf qu'on peut avoir un triangle équilatéral dont l'un des sommet est le centre du cercle et dont la longueur des cotés est égale au rayon...
est ce qu'on parle d'un triangle équilatéral dont le barycentre est le centre du cercle ? ou est ce qu'on parle d'un triangle qui s'inscrit tout aussi bien dans le cercle mais dont l'un des sommet est le centre du cercle et dont les cotés sont de la longueur du rayon...?
20/06/2015 à 14h22
Je crois que le triangle doit etre inscrit dans le cercle, c a dire tous les points d'angle touchent la circonférence. On garde le dessin de growly!
20/06/2015 à 14h55
adhoc écrivait:
---------------
> Je crois que le triangle doit etre inscrit dans le cercle, c a dire tous les
> points d'angle touchent la circonférence. On garde le dessin de growly!
c'est ça
et sa solution est de déterminer toutes les cordes possibles à partir d'un point sur la circonférence, on obtient bien 1/3
mais si on détermine toutes les cordes possibles en translation... ? ça donne quoi ? :-)
==
[90% d'avoir au moins 2 personnes avec la même date anniversaire dans un groupe = 41 personnes]
la formule est une simplification de l'itération, puisqu'on cherche la probabilité inverse de "personne n'a le même anniversaire"; soit au premier 365 chances sur 365, au 2eme : 364 chances sur 365 et au troisieme, 363 chances sur 365, etc. soit :
365/365*364/365*363/365 (p fois) ce qui fait bien
A(365,p) / 365^p
Avoir toutes les itérations dans l'ordre de p dates sur 365 ne répond pas au raisonnement, selon moi...
============== cite ================
L'arrangement A (365,N) nous donne le nombre de tous les N_uplets de dates sur 365 dates, ces N uplets ayant des valeurs différentes (avec ordre!). C'est l'inverse de ce qu'on cherche
============== cite ================
puisque tu n'as bien sur pas fait 1-A(365,p)
du coup j'ai du mal a saisir comment tu es arrivé à cette formule ? (1- A(365,p) / 365^p)
--
Le mieux est l'ennemi du bien et Seule la mode se démode.
20/06/2015 à 15h31
ba A(365,p) , je l'ai écrit et expliqué, designe l'ensemble des p_uplets DIFFERENTS et en effet dans l'ordre
365^p , c'est l'ensemble de TOUS les p_uplets, qu'ils soient differents OU égaux.(en informatique, on parle de produit cartésien)
La proba d'elements differents est donc
A(365,p)/365^p
Donc la proba d'elements identiques est l'inverse
1-A(365,p)/365^p
20/06/2015 à 16h53
OKOK, c'est moi qui suis mal réveillé, puisqu'il est question de proba et pas de dénombrement :-) (pour le /365^p)
ça n'en permet pas non plus la résolution directe, mais bon
c'est plus élégant que le raisonnement itératif
--
Le mieux est l'ennemi du bien et Seule la mode se démode.
20/06/2015 à 21h34
Arf.
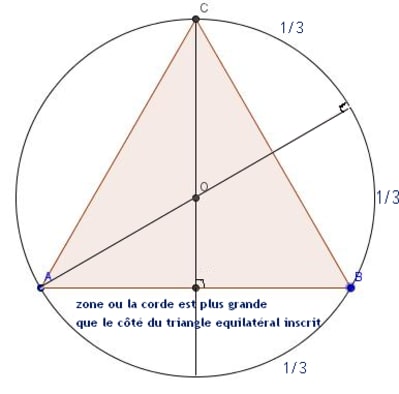
Pour le problème du triangle equilateral, ce dernier existe avec 3 angles de 60 degrés. On peut aussi considérer le tracé de 3 cordes de longueur identique quand on trace ce triangle.
Une corde du cercle trigonométrique est plus grande que celle décrite par un des angles du triangle, quand son angle d'ouverture est compris entre 60 degrés (exclus) et 90 degrés (inclus).
Pour simplifier , on découpera l'ensemble des cordes du cercle en sous ensembles caractérisés par le degré d'ouverture (espace discret)
On admettra qu'il existe une une equiprobabilité de tirage de ces cordes. Une corde de 20 degrés a autant de chances de sortir qu'une corde de 5 degrés ou de 60 degrés.
L’échantillon "cordes de moins de 60° fait le double de l'echantillon " cordes de plus de 60° et de moins de 90 °"
On peut dire alors que la probabilité pour qu'une corde d'un cercle, prise au hasard, soit plus grande que le côté du triangle équilatéral inscrit est de 1/3: p+2p=1
1/3 + 2*1/3=1
20/06/2015 à 21h57
11 joueurs de foot se font enfermés par leur entraineur, chacun dans leur chambre, à double tour... Leurs téléphones portables sont confisqués et ils n'ont aucun moyen de communiquer les uns avec les autres, ni avec autrui.
L'entraineur propose un jeu : s'ils gagnent, ils seront libérés sinon ils seront tous vendus à une autre équipe encore plus pourri!
Le principe du jeu est le suivant. Chaque jour, un des joueurs de foot est choisi aléatoirement pour aller dans une salle. Le hasard désignant le joueur qui va dans la salle, celui peut venir plusieurs fois, même à la suite.
A l’intérieur de cette salle, il n’y a qu’une ampoule et un interrupteur permettant de l’allumer et de l’éteindre. Le joueur de foot peut allumer la lumière, l’éteindre ou ne rien faire. Il ne peut rien faire d’autre dans cette salle et ne peut pas toucher l’ampoule. Seuls les joueurs de foot peuvent appuyer sur l’interrupteur. Au début du jeu, l’ampoule est éteinte et les joueurs de foot le savent.
Pour gagner le jeu, l’un des joueurs de foot doit pouvoir dire « tous les joueurs (les 11) sont passés au moins une fois dans cette salle » et que ça soit vrai.
Juste avant de débuter ce jeu, les 11 joueurs ont le droit exceptionnellement de discuter ensemble pendant quelques minutes afin d’établir une stratégie. Ce sera la seule fois.
Comment doivent-ils faire, pour ne pas se retrouver dans une équipe encore plus pourris ?!
ps : j'ai demandé à mes neveux de ne pas donner la solution à Enlay... Il va devoir sortir ses boules magiques :-)
21/06/2015 à 02h14
Ou la j arrive a peine , j'fini le restau ( cad je raque comme d' ab ) et j'vais chercher le ballon et les crampons :-))))
21/06/2015 à 12h00
j'ai fait un test pour le triangle:
5 PRINT "rayon du cercle ?"
10 INPUT R
20 PRINT R
30 PRINT "nombre de tests ?"
35 INPUT N
40 PRINT N
42 REM C = cote du triangle
43 C = R * SQR(3)
44 REM S=nombre de fois ou la corde est superieure au cote
45 LET S = 0
46 REM a = angle aléatoire
47 REM L = longueur de la corde
48 RANDOMIZE TIMER
50 FOR x = 1 TO N
60 a = RND * (3.14159265358979323846 * 2)
62 L = 2 * R * SIN(a / 2)
65 PRINT L
69 PRINT C
70 IF L > C THEN S = S + 1
80 NEXT
90 taux = S / N
100 PRINT taux
sur un test de N=2000000 je trouve 0.333452 :)
21/06/2015 à 12h11
Pour le triangle, oui, c'est 1/3 si on dénombre les cordes à partir d'un point sur la circonférence avec l'autre point choisi au hasard sur la circonférence.
mais j'ai demandé aussi... et si on dénombre les cordes en translation ? (son milieu sera un point du diametre)
--
Le mieux est l'ennemi du bien et Seule la mode se démode.
21/06/2015 à 13h22
foot ampoulé : y aurai bien une solution (que je ne vais pas spoiler) mais avec ce nombre de personnes, et avec une entrée par jour, on a 10!/11^20 de chances avant que tout le monde passe, c'est à dire en gros un temps incommensurablement bien au dela de l'âge de l'univers...
avec 4 personnes dont une passe toutes les minutes pour que ça reste humain ?
--
Le mieux est l'ennemi du bien et Seule la mode se démode.
22/06/2015 à 00h39
Pourtant le programme de growler, parfait, tire aléatoirement une corde etre deux points au hasard sur la circonférence du cercle
60 a = RND * (3.14159265358979323846 * 2)
(l'angle en radian est choisi au hasard entre 0 et 2 Pi, nickel, mon growly). le programme est muni d'un compteur S qui s'incrémente quand la longueur d'une corde prise au hasard depasse le coté du triangle (bon, allez,growly vire else S=S, c'est inutile!)
Cette méthode aléatoire, prise sur un tres grand nombre d'essais se rapprochera idéalement de la probabilité de la longueur de corde supérieure a la corde décrite par un des cotés du triangle équilateral.
Ce que tu veux dire, trymartin, c'est que de la façon dont on echantillonne les cordes géométriquement (radial, parallèle au diametre ), on pourrait avoir un résultat différent! Mettons!
Mais la méthode aléatoire de growly me semble la plus pure, non pour avoir le résultat exact , mais une valeur qui approche de très prés.
Ton probleme de footballeurs est affreux! L'informatique, c'est aussi des interrupteurs (ouvert, fermé) , mais on a des piles, sortes de compteurs qui entassent les valeurs processeur.
Il y a peut etre cette notion dans ton énigme , mais c'est trop casse tete, notre cerveau n'est pas un circuit logique!
22/06/2015 à 01h18
adhoc écrivait:
---------------
> Ton probleme de footballeurs est affreux! L'informatique, c'est aussi des
> interrupteurs (ouvert, fermé) , mais on a des piles, sortes de compteurs qui
> entassent les valeurs processeur.
> Il y a peut etre cette notion dans ton énigme , mais c'est trop casse tete,
> notre cerveau n'est pas un circuit logique!
>
La solution est pourtant simple : cette fois-ci, il n'y a aucune équation compliquée à résoudre.
Et, si tu y réfléchis un peu, tu trouveras facilement la RAM (Random Access Memory) dont tu as besoins... ;-)
22/06/2015 à 01h34
La nuit porte conseil, j'y reflechirai, mon carident (ton enigme est "affreuse" mais je dis cela dans un sens positif!). Un ou deux joueurs doivent en effet servir de mémoire compteur, mais comment? Et quelle est leur action sur le compteur? Et quelle est l'action menée sur l'interrupteur? (faut pas le griller!)
Un ingé informaticien "systeme" devrait trouver...
A voir....
J'essaierai avec 4 joueurs, c'est plus facile!
Bon, on les numerote, ca c'est sur!
Admettons qu'on ait
1,2,1,1,3,2,4,
Ca devrait s'arreter car les 4 joueurs sont passés dans la piece, ou peut etre attendre le passage du ou des deux joueurs "pile".
C'est difficile....
22/06/2015 à 01h59
ba , la , je l'ai brulé trois fois dans mes essais, pffff :-)
Je m'y remets demain soir, sauf si c'est trouvé . Et ca serait chouette que celui ou celle qui trouve reprenne mon exemple avec quatre joueurs et nous montre que l'equipe ne sera pas déclassée :-)
22/06/2015 à 03h45
adhoc écrivait:
---------------
" Admettons qu'on ait 1,2,1,1,3,2,4,
Ca devrait s'arreter car les 4 joueurs sont passés dans la piece, ou peut etre attendre le passage du ou des deux joueurs "pile"."
tu entends quoi par pile ?
22/06/2015 à 07h50
adhoc écrivait:
---------------
> Ce que tu veux dire, trymartin, c'est que de la façon dont on echantillonne les
> cordes géométriquement (radial, parallèle au diametre ), on pourrait avoir un
> résultat différent
ben calcule :
- on prend un point et tous les angles
(ou avec l'ensemble de tous les points de départ, ce qui revient à choisir 2 points au hasard, ça ne change pas la solution)
- on prend le centre sur le diametre (ou avec l'ensemble de tous les diamètres)
- on prend le centre sur une surface (on définira évidemment la surface ou toutes les cordes sont plus grandes qu'un côté d'un triangle inscrit)
dans les trois cas on a bien toutes les cordes possibles et les resoudre : c'était ça mon enigme et pas que la première partie, je voulais la diluer, mais a l'evidence ma sauce ne prend pas...
===
foot ampoulé : effectivement tu brûles, voyons si tu trouves la même proba improbale (pour 11 personnes) qui mène à la résolution ...