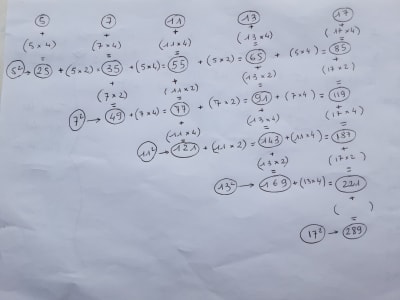Tous les forums
Je cache un trésor
10/02/2023 à 10h29
OK je t’envoie ça avec des modifs d’hier soir dans 15 min environ
10/02/2023 à 16h34
On prend 169, une des valeurs que tu as encadrées.
On a sur ton schema
11²+(11*2)+(13*2)=169
Soit le développement de (11+2)² lol !!!!!
Et il faut aller chercher a partir de 11, le nombre premier suivant (13) pour avoir le carré. Pas vraiment ce qu'on veut!Sauf si on peut tourner toujours le cadran horaire avec les memes valeurs.
Mefie toi quand meme, la recherche d'algorithmie des nombres premiers est épuisante mentalement, les plus grands mathematiciens s'y cassent toujours les dents.
10/02/2023 à 19h37
adhoc écrivait:
-----
> On prend 169, une des valeurs que tu as encadrées.
> On a sur ton schema
> 11²+(11*2)+(13*2)=169
>
> Soit le développement de (11+2)² lol !!!!!
> Et il faut aller chercher a partir de 11, le nombre premier suivant (13) pour
> avoir le carré. Pas vraiment ce qu'on veut!Sauf si on peut tourner toujours le
> cadran horaire avec les memes valeurs.
> Mefie toi quand meme, la recherche d'algorithmie des nombres premiers est
> épuisante mentalement, les plus grands mathematiciens s'y cassent toujours les
> dents.
Oui c’est exact mais je n’ai fait que comprendre les rapports existants entre les multiples .
Rien de plus sinon que je retourne ma feuille dans tous les sens.
Vire et vire.....tourne et retourne 🤣🤣🤣🤣🤣
10/02/2023 à 23h34
Salut adhoc,
Une seule question pour demain.
Est-ce que pour atteindre une rapidité d’exécution d’un programme il faut tendre au maximum vers une simplicité d’affichage ou de stockage dans un tableau qui ressemblerait à une sortie des nombres entier consecutifs vers un périphérique en utilisant au minimum une opération d’incrementation-affectation avec un compteur ?
11/02/2023 à 08h42
L'affichage, on s'en fiche.
Faire un tableau, on s'en fiche aussi.
Ce qui prend des ressources (temps) , c'est le nombre d' itérations pour une opération. Ainsi en est il de la determination des nombres premiers, A chaque nombre testé, il faut terster tous les diviseurs possibles sur sa racine carrée +1. Le programme en lui meme est super simple.
Donc au bout de quelques millions, il faut actuellement des super calculateurs . c'est un peu comme pour les echecs quand on faituintervenir l'analyse des coups possibles....
Dionc ressources: nombres d'iterations.
Ce que tu fais, tu mets un compteur de temps en debut et fin d'operations. Fais un programme de determination des nombres premiers, methode brute (la seule actuelle) , va a plusieurs centaines de milliers et chronometre.
Puis ton algo a toi, si tu en trouves un, chronometre aussi et compare. C'est la seule methode valable.
11/02/2023 à 09h06
Le chrono sur qq milliers de NP j’y ai pensé
J’ai ma réponse collègue, merci.
A+
11/02/2023 à 09h09
Quelques centaines de milliers, sinon la comparaison n'est pas valable. Le delta serait trop faible entre l'algo classique et le tien.
Perso, je fais tout en php (et javascript quand necessaire). L'avantage, c'est qu'on peut tester sur serveur et montrer a n'importe qu à distance.
12/02/2023 à 12h47
adhoc écrivait:
-----
> Quelques centaines de milliers, sinon la comparaison n'est pas valable. Le
> delta serait trop faible entre l'algo classique et le tien.
> Perso, je fais tout en php (et javascript quand necessaire). L'avantage, c'est
> qu'on peut tester sur serveur et montrer a n'importe qu à distance.
Php ça ressemble au C mais il faut installer un serveur local sur sa becanne.
En plus on se sert d’un éditeur classique et on crée une page en extension html.
Je l’avais déjà utilisé pour des pages Web dynamique.
Je vais voir en tout cas.
Merci.
J’ai trouvé ça sur Android avec un didacticiel et un interpréteur de commande.
On peut exécuter apparemment sans installation supplémentaire.
Ça va être sympa je pense.
Merci pour l’idée.
https://play.google.com/store/apps/details?id=com.os.phpviewer.viewphpfiles.phpreader.phpfileviewer
14/02/2023 à 06h40
adhoc écrivait:
-----
> Hello , voici mon programme en langage universel qui doit determiner si ta
> fonction horaire liste tous les nombres premiers, au moins jusqu'a 1000 (on ira
> plus loin apres, mais ca va ramerun peu)
> Verifie la, si ca te va, je le mets en Php et le fais tourner
>
> ________________________________________________________________
> Declatation du tableau LIST_PREMIER : tableau qui contient les 1000 premiers
> nombres premiers
> Declaration de la fonction EST_PREMIER (teste si un nombre est premier)
>
> Declaration du tableau FONCTION (contenu des operations recursives )
> Declaration de la fonction COMPARE_TABLEAUX (compare le tableau obtenu par les
> fonctions et le tableau des nombres premiers)
>
> x=1
> Pour compteur allant de 3 vers 1000
> {
>
> Si EST_PREMIER(x)
> {
> SI n'appartient pas au tableau FONCTION()
> {
> FONCTION[]=x
> }
>
> }
>
> x=x+12
> }
>
> x=5
> Pour compteur allant de 3 vers 1000
> {
>
> Si EST_PREMIER(x)
> {
> SI n'appartient pas au tableau FONCTION()
> {
> FONCTION[]=x
> }
>
> }
>
> x=x+12
> }
>
> x=7
> Pour compteur allant de 3 vers 1000
> {
>
> Si EST_PREMIER(x)
> {
> SI n'appartient pas au tableau FONCTION()
> {
> FONCTION[]=x
> }
>
> }
>
> x=x+12
> }
>
> x=11
> Pour compteur allant de 3 vers 1000
> {
>
> Si EST_PREMIER(x)
> {
> SI n'appartient pas au tableau FONCTION()
> {
> FONCTION[]=x
> }
>
> }
> x=x+12
> }
>
> COMPARE_TABLEAUX()
> LISTER les nombres premiers qui ne sont pas dans FONCTION
EUREKA MAIS C’EST BIEN SÛR !!!!!
Si ton programme à un petit détail près donnait dans la meme boucle les nombres multiples et en même temps les diviseurs premiers de ces multiples .......est-ce qu’on aurait tout bon (et sans faire aucune division ni multiplications supplémentaires ?????
Parceque si c’est le cas ben je t’envoie la solution en MP.
ET C’EST TOUT CON MON VIEUX.
A+
14/02/2023 à 08h47
Ba non, mon programme n'a rien d'intelligent, helas. Il se contente de verifier si ton algorithme laisse passer des nombres premiers. ...
Il n'en laisse pas si on compare avec l'algorithme, tres tres lourd, officiel de dedermination des nombres premiers.
Mais il n'y a a ma connaissance STRICTEMENT aucun moyen d'enlever les multiplicateurs parasites par des fonctions inverses des tiennes.....
Ecris ton algo en langage universel (declarations, conditions, boucles) et je le programmerai.
14/02/2023 à 09h22
adhoc écrivait:
-----
> Ba non, mon programme n'a rien d'intelligent, helas. Il se contente de verifier
> si ton algorithme laisse passer des nombres premiers. ...
> Il n'en laisse pas si on compare avec l'algorithme, tres tres lourd, officiel de
> dedermination des nombres premiers.
> Mais il n'y a a ma connaissance STRICTEMENT aucun moyen d'enlever les
> multiplicateurs parasites par des fonctions inverses des tiennes.....
>
> Ecris ton algo en langage universel (declarations, conditions, boucles) et je le
> programmerai.
Pas encore je veux voir jusqu’où ça tient la route.
Déjà on élimine les test avec les tableaux qui ne servent plus à rien.
Ensuite
Il faut changer les incrementations des x en commençant par 5 et non par 1
Soient x = 5
x= 7
x= 11
x= 13
On change l’écriture des nombres décimaux dans ces développements
Pour x=5 on sort la conversion du nombre P que l’on rentre et on l’écrit en base 5.
De cette façon tous les multiples de 5 se termineront par 0 et seront traçable facilement.
Donc
x=5 ==> conversion en base 5 ou x mod(5)
Idem x=7 ==> conversion en base 7 ou x mod(7)
Idem x=11 ==> 11 ou x mod(11)
Idem x=13 ==> ’ 13 ou x mod(13)
Base 10 : 5 7 11 13 17 19 23 (25) 29 31 (35) 37 41 43 47 (49) 53 (55)
Base 5 : 10 12 21 23 32 34 43 (50) 54 61 (70) 72 81 82
Base 7 : 5 10 14 16 23 15 32 34 41 43 (50) 52 56 61 63 (70)
Base 11 : 5 7 10 12 16 18 21 23 27 29 32 34 38 3A 43 45 49 (50)
Base 17 : etc etc etc
Déjà on observe que chaque fois que quand le mod (x) se termine par 0 on a un multiple qui peut déjà être repéré sans multiplication dans la chaine en Base10
Pour x = 5 et l’opération d’affectation x = x +12 :
on voit 50 base⁵ = 25 qu’on supprime
et 70 base⁵ = 35 qu’on supprime également
Pour x = 7 .............................
on voit 50 base⁷ = 35 qu’on supprime
on voit 70 base⁷ = 49 qu’on supprime
Pour x = 11 .............................
on voit 50 base¹¹ = 55 qu’on supprime Etc etc
On peut même imaginer avoir sur la même colonne 2 nombres se terminant par 0 et cela donnerait le résultat d’une recherche inverse qui consisterait à partir d’un nombre x en lecture dans la base 10 à retrouver ses multiples p1et p2 (x = p1×p2).
Bien entendu
5 base ⁵ = 10
7 base⁷ = 10
11 base¹¹ = 10 ne comptent pas
etc etc etc
Le seul problème est qu’à priori il faudra calculer les modulos de tous les P suivants 17 !!!!!
14/02/2023 à 11h53
lol tu es finalement, sans le savoir , en train de programmer l'existence (ou la liste) , d'un nombre premier avec la methode traditionnelle qui tient sur quelques lignes, mais qui est extrêmement consommatrice en resources si tu etablis la liste, a partir du 100000 eme( ou plus, selon la capacité de calcul du proc/carte graphique)
Tester tous les modulos est horrible, mais on n'a riebn d'autre pour le moment.....
Le programme est, lis le BIEN
//Cette fonction teste si le nombre est premier ou non
function siPremier($nombre)
{
if ($nombre == 1)
return 0;
for ($i = 2; $i <= sqrt($nombre); $i++){
if ($nombre % $i == 0) //si le modulo du nombre avec le diviseur en cours egale 0
return 0; //la fonction n'est pas validée (on est en presence d'un multiple
}
return 1;//la fonction est validée, ON EST EN PRESENCE D4UN NOMBRE PREMIER
}
Et c'est tout !!!! Quelques lignes qui y arrivent a des nombres tpremiers res grands, mais assez betes.....ON nA RIEN D AUTRE....
L'Humain a ses limites.....
14/02/2023 à 12h57
adhoc écrivait:
-----
> lol tu es finalement, sans le savoir , en train de programmer l'existence (ou la
> liste) , d'un nombre premier avec la methode traditionnelle qui tient sur
> quelques lignes, mais qui est extrêmement consommatrice en resources si tu
> etablis la liste, a partir du 100000 eme( ou plus, selon la capacité de calcul
> du proc/carte graphique)
> Tester tous les modulos est horrible, mais on n'a riebn d'autre pour le
> moment.....
>
>
> Le programme est, lis le BIEN
> //Cette fonction teste si le nombre est premier ou non
> function siPremier($nombre)
> {
> if ($nombre == 1)
> return 0;
>
> for ($i = 2; $i <= sqrt($nombre); $i++){
> if ($nombre % $i == 0) //si le modulo du nombre avec le diviseur en
> cours egale 0
> return 0; //la fonction n'est pas validée (on est en presence d'un
> multiple
> }
> return 1;//la fonction est validée, ON EST EN PRESENCE D4UN NOMBRE PREMIER
> }
>
> Et c'est tout !!!! Quelques lignes qui y arrivent a des nombres tpremiers res
> grands, mais assez betes.....ON nA RIEN D AUTRE....
> L'Humain a ses limites.....
Mède alors se !!!!! y a plus qu’à aller prendre le soleil.🤣🤣🤣🤣
Nb il me reste un détail à voir pour passer le temps. Tous les P² se trouvent sur le même axe 0-1 sur l’horloge????
01/03/2023 à 20h46
Devinette:
En enlevant une seconde d’arc à Zeta de 2 on tombe sur l’égalité suivante = 👹× Pi
Zeta étant la fonction d’Euler en x =2 ou Zeta(2)
Rien que ça tiens,tiens,tiens 🤩🤩🤩!!
Venez donc me chercher.
07/02/2024 à 21h32
Plus scientifique tjs avec Jean Staune
?si=Y2b7ZmvEfuAC92b-
12/04/2024 à 06h03
adhoc écrivait:
-----
> prends pas ca, mais si tu veux programmer a l'ancienne en basic, VB5 ou VB6.
> J'ai une version tombée du camion d'un CD Visual Studio qui contient toute la
> suite VB, Delphi, visual C++, visual fox pro.
> Je te conseille quand meme, pour etre portable de te mettre a Visual C++. Ca
> passe encore dans les ordis actuels, et tu auras des bonnes bases de
> développement.
> MP si tu es interessé, jez te mets l'ISO (image du CD) sur un serveur avec un
> mot de passe htaccess.
> Mais si tu veux programmer pour de l'internet, je te conseille php et
> javascript, ou Android studio (JAVA) pour les telephones portables. Tout est
> alors gratuit.
Ton C++ m’intéresse adhoc stp.
11/11/2024 à 05h30
VITESSE DE LA LUMIÈRE :
Pourquoi la vitesse de la lumière est elle infranchissable?
Au delà des réponses habituelles de RG il existe une réponse qui donne une idée bien plus intuitive de ce fait et qui est bien moins connue. J’en ai fait la découverte il y a seulement 24 heures et j’en suis resté scotché! Et pourtant elle est si évidente quand on y pense. Pur moment de plaisir pour moi en tout cas.
Pour trouver cette réponse " intuitive" il faut chercher un synonyme équivalent à la vitesse de la lumière............
...............?
11/11/2024 à 08h32
Si tu vas plus vite que la lumière c'est plus éclairé, alors t'y vois plus rien, à la limite t'existes plus.😁
11/11/2024 à 09h50
vulpi écrivait:
-----
> Si tu vas plus vite que la lumière c'est plus éclairé, alors t'y vois plus rien,
> à la limite t'existes plus.😁
Je suis sûr que tu as dû faire l’expérience en vélo de nuit en pédalant trop fort!!!!
On sent que c’est du vécu ce truc. 👏👏👏👏🤔🤔
11/11/2024 à 12h30
Grifix-Gezucri écrivait:
--------------
...
> Pourquoi la vitesse de la lumière est elle infranchissable?
...
Parce qu'on n'est pas des lumières, en clair (gag !) on est trop cons.
Bon après perso, rien à cirer de la franchir, suis pas pressé à ce point.
11/11/2024 à 13h10
Certains phénomènes, comme l'intrication quantique, semblent défier l'idée de transmission de l'information à une vitesse limitée. Dans l'intrication, deux particules entremêlées montrent des corrélations instantanées, indépendamment de la distance qui les sépare.
11/11/2024 à 13h35
Quelque soit la vitesse à laquelle tu te déplaces, la vitesse de la lumière est (une) constante, elle reste la vitesse de la lumière et ne peut être soustraite ou additionnée. Cad, si tu faisais la course avec "la lumière", tu cours à 2/3 de sa vitesse, quelle est la vitesse de la lumière que tu observes ? La vitesse de la lumière.
Donc indépassable, en théorie.