On fait péter le système bancaire Adhoc !!!!!

Un graphique parfaitement symétrique qui englobe tous les nombres non premiers parfaitement alignés et à l’exception de ces derniers bien sûr c’est intéressant ou pas Adhoc🤣🤣🤣🤣?

Pour l’instant je n’ai que des suites d’exclusion qui ne sont pas forcément exhaustives sur les
Non premiers, mais mis à part 2 5 7 au démarrage se suis quasi certain que les 4 suites et suivantes par extension logique ( en incluant celle centrale des triangulaires ) ne contiennent pas de NP.

Screenshot_20220827-102040_ClevNote.jpg

Je suis arrivé à avoir toutes les suites exhaustives quei ne devraient contenir aucun nombres premiers mais seulement des pairs et impairs non premiers.
J’ai commencé un programme qui développe ces suites et un de test de primalite.
La construction de ces suites est très coherente et on devrait pouvoir faire un crible qui soit différent de Matiiassevitch et Eratosthene et réaliser un dessin géométrique correct .
A suivre donc.
Je rêve peut-être mais ça me coûte que du temps et à la retraite on peut se le permettre non?
( Il faut faire des corrections sur le diagramme en pièce jointe)

Demain je vérifierai si :
En posant T(i) comme étant le nombre triangulaire de rang i si la somme de toutes les suites
de rang i et d’incrementation d’indice i donnent bien tous les nombres pairs et impairs non premiers.(tables xtions)
Soit Somme des T(i) pour i = 3 à l’infini des T(i)+ i
Plus simplement il s’agit se faire
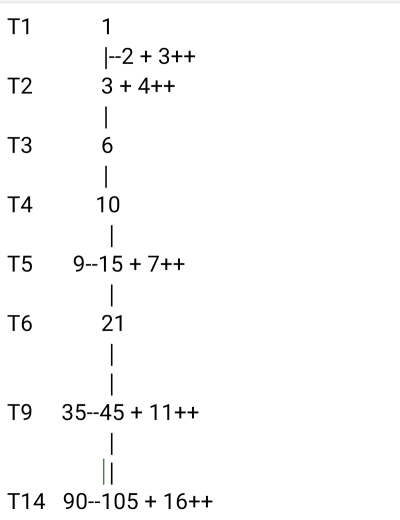
T(i) = i × (i +1) / 2 + i
Exemple
pour i = 3 , T(3) = 6
La suite sera : 6 9 12 15 etc
pour i = 4 , T(4) = 10
La suite sera : 10 14 18 22 etc
On obtient quand même un tableau semblable à la pièce jointe :
Curieux non ?
Une sorte de Eratosthene remis en ordre non?
Bonne nuit.

Screenshot_20220828-224936_ColorNote.jpg

Tous les nombres pairs premiers ou non sont uniquement sur la deuxième çolonne.
En éliminant les xtiples de 9 3 ou 5 on peu me semble t-il mener une recherche visuelle très rapide à proximité dans les tables multiplications. S’il est absent dans ces tables le nb est premier.........
Reste à chercher un algo de recherche sur ces tables.

On laisse tomber c’est une table de multiplications ce truc.
Donc impossible de trouver un premier.
Je vais me lire un Picsou et me détendre.

adhoc

01/09/2022 à 19h15

Pas tout a fait une table de multiplication.
J'ai fait le programme pour les 20000 premiers nombres triangulaires, en testant s'ils sont premiers.
Aucun n'est premier dans cette grosse série 'sauf le premier ecidemment)
Pour faire peter la banque , c'en est loin. Mais ca reste interessant pour éliminer une partie des nombres non premiers avec un algorithme beaucoup moins consommateur de ressources.

https://reduction-image.com/eugenol/triangles_griffix/index3.php

adhoc écrivait:
-----
> Pas tout a fait une table de multiplication.
> J'ai fait le programme pour les 20000 premiers nombres triangulaires, en
> testant s'ils sont premiers.
> Aucun n'est premier dans cette grosse série 'sauf le premier ecidemment)
> Pour faire peter la banque , c'en est loin. Mais ca reste interessant pour
> éliminer une partie des nombres non premiers avec un algorithme beaucoup moins
> consommateur de ressources.
>
> https://reduction-image.com/eugenol/triangles_griffix/index3.php

Screenshot_20220829-224148_ColorNote.jpg

Screenshot_20220829-231016_ColorNote.jpg

Screenshot_20220829-232014_ColorNote.jpg

9bd6988e-336d-4962-8201-5b0d01313c60.jpeg

Screenshot_20220829-222603_ColorNote.jpg

Suite....
On voit que pour créer les suites les multiplications entre colonne1 et colonne 2
se font en ligne oblique pui en ligne horizontale.
On obtient le premier nombre triangulaire
Quand on multiplie en oblique on obtient la première colonne
2×3=6 +3+3+3+3+3+3+3+3
Quand on multiplie en ligne on obtient
3×7=21+(7-1)+(7-1)+(7-1) etc etc
Et ainsi de suite

Screenshot_20220901-210452_ColorNote.jpg

Prolongement...

Screenshot_20220901-204921_ColorNote.jpg

ils ont de l'endurance jusqu'au bout de la nuit!!!!

groggy.JPG

Fais de beaux rêves ma grande ...... je te veille n’aie pas peur🧚🧚‍♀️

J’en ai profité comme je dors pas de m’amuser un peu et de fil en aiguille on devrait tirer un
Algorithme sympa de ce tableau très logique dans sa construction
Réf 3 Saisies d’écrans successives.

Screenshot_20220902-052857_ColorNote.jpg

Screenshot_20220902-052848_ColorNote.jpg

Screenshot_20220902-052904_ColorNote.jpg

Je verrai par la suite à supprimer la première colonne multiple de 3 inutile.
En la supprimant il faudra tester si le nb est divisible par 3 ainsi que sa racine carrée et sa divisibilite par 9.
A force de vouloir supprimer des suites il me manque les puissances de 7


--
Nè le 11 septembre 1958 décédé le 11 novembre 2023 🤪

Conclusion :
L’addition de n nombres entiers consecutifs quand n est > ou = à 3 ne donne jamais un nombre premier.

n + (n+1) + (n+2)+.....+(n+p) = (p+1)(2n +p) / 2
Si p est pair ==> 2n+p est pair ==>le résultat de l’équation est un entier non premier
Si p est impair p+1 est pair ==> le résultat de l’équation est également un entier non premier.

Exemple : 7 +8+9+10+11 + 12 = 57 Non Premier ( 57÷3= 19)